Algorithme de Prim

Dans ce didacticiel, vous apprendrez comment fonctionne l'algorithme de Prim. Vous trouverez également des exemples fonctionnels de l'algorithme de Prim en C, C ++, Java et Python.

L'algorithme de Prim est un algorithme d'arbre couvrant minimum qui prend un graphique en entrée et trouve le sous-ensemble des arêtes de ce graphique qui

forme un arbre qui inclut chaque sommet
a la somme minimale de poids parmi tous les arbres qui peuvent être formés à partir du graphique

Comment fonctionne l'algorithme de Prim

Il appartient à une classe d'algorithmes appelés algorithmes gloutons qui trouvent l'optimum local dans l'espoir de trouver un optimum global.

Nous partons d'un sommet et continuons d'ajouter des arêtes avec le poids le plus bas jusqu'à ce que nous atteignions notre objectif.

Les étapes de mise en œuvre de l'algorithme de Prim sont les suivantes:

Initialisez l'arbre couvrant minimum avec un sommet choisi au hasard.
Trouvez toutes les arêtes qui relient l'arbre à de nouveaux sommets, trouvez le minimum et ajoutez-le à l'arbre
Continuez à répéter l'étape 2 jusqu'à ce que nous obtenions un arbre couvrant minimum

Exemple d'algorithme de Prim

Commencez par un graphe pondéré

Choisissez un sommet

Choisissez l'arête la plus courte de ce sommet et ajoutez-la

Choisissez le sommet le plus proche pas encore dans la solution

Choisissez l'arête la plus proche pas encore dans la solution, s'il y a plusieurs choix, choisissez-en une au hasard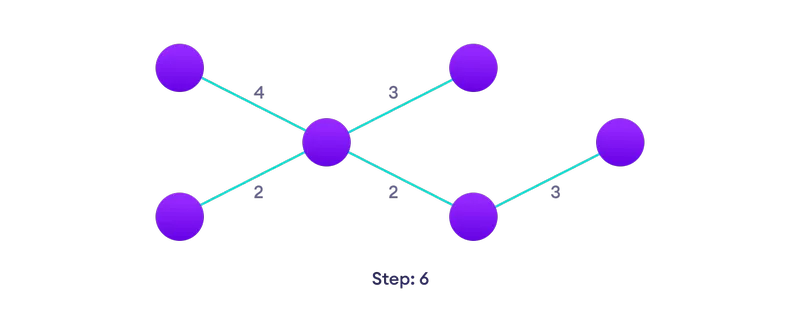

Répétez jusqu'à ce que vous avoir un arbre couvrant

Pseudocode de l'algorithme de Prim

Le pseudocode de l'algorithme de prim montre comment nous créons deux ensembles de sommets U et VU. U contient la liste des sommets qui ont été visités et VU la liste des sommets qui ne l'ont pas été. Un par un, nous déplaçons les sommets de l'ensemble VU vers l'ensemble U en connectant l'arête la moins pondérée.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Exemples Python, Java et C / C ++

Bien que la représentation matricielle d'adjacence des graphiques soit utilisée, cet algorithme peut également être implémenté à l'aide de la liste d'adjacence pour améliorer son efficacité.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Algorithme de Prim vs Kruskal

L'algorithme de Kruskal est un autre algorithme d'arbre couvrant minimum populaire qui utilise une logique différente pour trouver le MST d'un graphe. Au lieu de partir d'un sommet, l'algorithme de Kruskal trie toutes les arêtes de faible poids à élevé et continue d'ajouter les arêtes les plus basses, ignorant les arêtes qui créent un cycle.